TPE 2k4

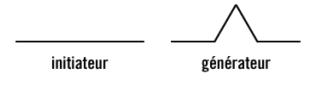
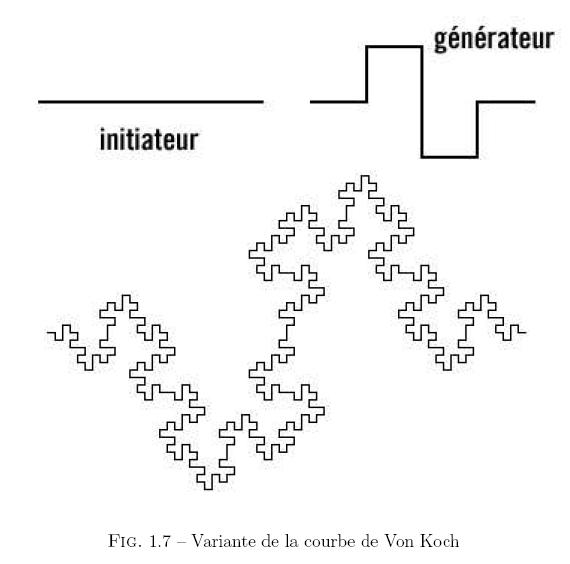
Pour mieux percevoir ce qu'est une fractale, la construction de d'une courbe fractale peut s'avérer utile. On utilise un exemple célèbre, la courbe de Von Koch, comme représentation de la construction d'un objet fractal. Elle nécessite deux formes géométriques de départ qui sont l'initiateur et le générateur :

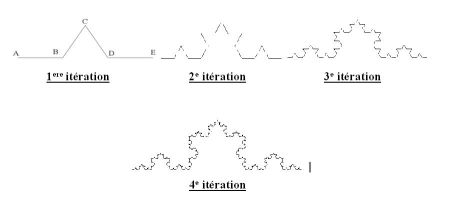
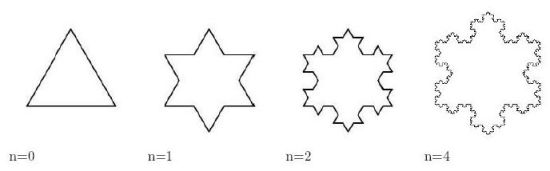
A partir de l'initiateur, on remplace chaque segment par une figure géométrique de même forme que le générateur. Chaque étape est une itération : on réitère cette méthode une fois, deux fois, …, n fois, jusqu'à obtenir une courbe fractale :

Mais l'épaisseur du trait et la taille des segments limitent la suite de la construction. On se propose maintenant de calculer la dimension fractale de la courbe de Von Koch à partir de la formule de Mandelbrot vue précédemment :
-on choisit un étalon d'une longueur l = x d'un segment de la première itération (l = AB).
-cet étalon est reporté donc n = 4 fois lors de la première itération.
-la courbe a la longueur du segment AE donc L = 3x (car AE = AB+BD+DE).
Nous avons donc : d = ln 4 / ln (3x/x)
d = 2ln 2 / ln 3
ainsi d =1,26186

Ce résultat peut aussi être vérifié lors de la seconde itération : l'étalon utilisé est toujours de la longueur d'un segment donc l = x, mais il est reporté n = 16 fois et L = 9x :

Donc d = ln 16 / ln (9x/x)
d= ln (24) / ln [(32x)/x]
d= 4ln 2 / 2ln 3
d =1.26186

Différentes variantes de la courbe de Von Koch existent, il suffit pour cela de changer le générateur, ainsi avec celui ci :

Mais Von Koch est principalement connu pour son " flocon ", il s'agit du regroupement de trois courbes de Von Koch sous la forme d'un triangle :

Webmaster : Aurélien Courant